Actualités

Le concept d’universalité fait référence à l’un des phénomènes physiques les plus déconcertants que l’on puisse trouver dans la nature. Il décrit le fait que lorsqu’un système complexe à N corps est amené à proximité d’une transition de phase, c’est-à-dire près d’un point critique, son comportement devient indépendant des détails du système, de sorte qu’il est possible de trouver d’autres systèmes sans aucun lien entre eux qui présentent exactement le même comportement, c’est-à-dire qui sont décrits par le même modèle mathématique.

L’équation de Kardar, Parisi et Zhang (KPZ) est l’un de ces modèles ; elle décrit correctement, par exemple, la forme d’un front d’incendie qui se propage, la forme du bord d’une colonie de bactéries en expansion ou la rugosité de l’interface d’un cristal en croissance. Dans ce travail dans le cadre d’une collaboration internationale d’expérimentateurs et de théoriciens, nous avons montré que dans un condensat de polaritons unidimensionnel – une réalisation expérimentale d’un condensat « driven-dissipative » de particules semblable à des photons, et piégées dans une microcavité unidimensionnelle – les fluctuations stochastiques de la phase du condensat présentent toutes les signatures clés de la classe d’universalité de KPZ. Par exemple, après une remise à l’échelle adéquate, les données expérimentales des corrélations de phase spatio-temporelles se retrouvent toute alignées selon la fonction d’échelle universelle KPZ.

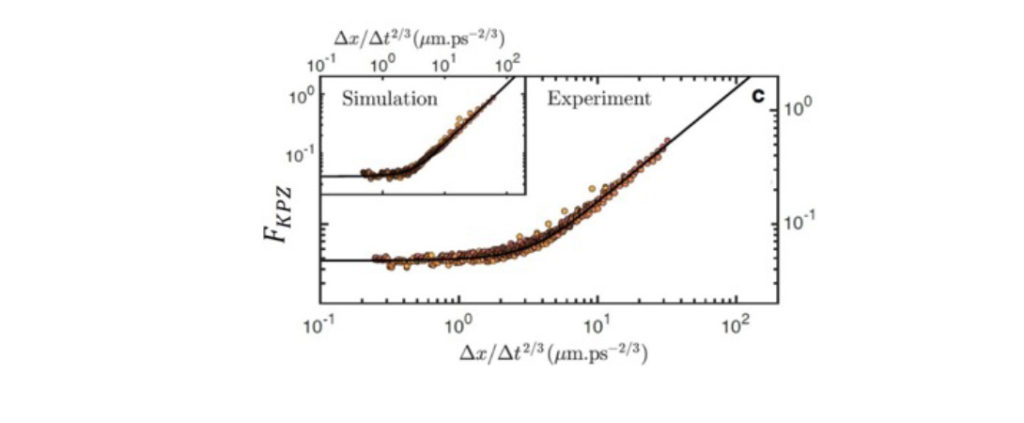
Ce résultat révèle une différence de nature essentielle entre un tel condensat « driven-dissipative » et son homologue en équilibre thermique. Notre analyse microscopique montre que ce régime KPZ est également pertinent pour les systèmes lasers à modes étendus spatialement, avec un fort impact technologique potentiel pour leur optimisation. D’un point de vue plus fondamental, nous pouvons maintenant élargir notre étude expérimentale de KPZ aux condensats bidimensionnels, une géométrie très mal connue en raison du défi qu’elle pose d’un point de vue théorique.

Quentin Fontaine, Davide Squizzato, Florent Baboux, Ivan Amelio, Aristide Lemaître, Martina Morassi, Isabelle Sagnes, Luc Le Gratiet, Abdelmounaim Harouri, Michiel Wouters, Iacopo Carusotto, Alberto Amo, Maxime Richard, Anna Minguzzi, Léonie Canet, Sylvain Ravets & Jacqueline Bloch

Nature 608, 687–691 (2022) Kardar–Parisi–Zhang universality in a one-dimensional polariton condensate