- Home
- Institut Néel
- Research teams
- Technical Groups & Services
- Work at the Institut
- Partnerships
Le concept d’un
The concept of Universality refers to one of the most puzzling physical phenomenon one can find in nature. It describes the fact that when a complex many-body system is brought close to a phase transition, i.e. close to the so-called critical point, its behaviour becomes independent from the system details, such that other completely unrelated systems can be found that exhibit the exact same behaviour, i.e. described by the same mathematical model.
The Kardar, Parisi, and Zhang (KPZ) equation is one such model; It describes correctly for instance, the shape of a propagating fire front, the edge shape of a thriving colony of bacteria, or the interface roughness of a growing crystal. Now, within an international collaboration of experimentalists and theoretists, we have shown that in a one-dimensional polariton condensate – an experimental realization of driven-dissipative condensate of photon-like particles trapped in a 1D microcavity – the stochastic fluctuations of the condensate phase exhibit all the key signatures of the KPZ universality class. For instance, upon adequate rescaling, the space-time phase correlations datapoints can all be found to collapse onto the KPZ universal scaling function.
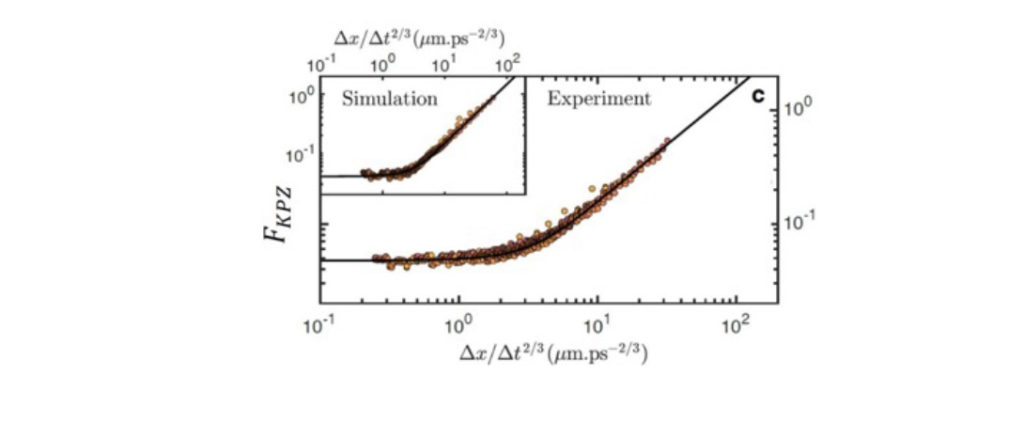
This result reveals a key difference of nature between such a driven-dissipative condensate and its thermal equilibrium counterpart. Our microscopic analysis also shows that this KPZ regime is also relevant to spatially extend lasers system with potential technological impact in their optimization. On a more fundamental side, we can now extend our experimental investigation of KPZ to two-dimensional condensates, a geometry which is highly sought for due to the challenge it poses in theoretical analysis.
Quentin Fontaine, Davide Squizzato, Florent Baboux, Ivan Amelio, Aristide Lemaître, Martina Morassi, Isabelle Sagnes, Luc Le Gratiet, Abdelmounaim Harouri, Michiel Wouters, Iacopo Carusotto, Alberto Amo, Maxime Richard, Anna Minguzzi, Léonie Canet, Sylvain Ravets & Jacqueline Bloch
Nature 608, 687–691 (2022) Kardar–Parisi–Zhang universality in a one-dimensional polariton condensate
