Équipe de recherche
Ultra-low temperatures
Fundamental research at the ultra-low temperature frontier
Goals
The ULT team performs condensed matter experiments down to the microkelvin temperature range. We study model systems and develop the state-of-art techniques required by these demanding experiments, building on the capabilities of the Néel laboratory. The physics involved concerns quantum fluids, amorphous matter and fundamental aspects of microwave opto-nano-mechanics. The group is part of the European Microkelvin Platform, a “laboratory without walls” federating ultra-low temperature physics at the European level.
 |
WebMaster: E.C.&A.F. 2023 |
Micro/Nano-mechanics
Currently there is great enthusiasm for the experimental realization and study of MEMS (micro-electro-mechanical-systems) and the even smaller NEMS (nano-electro-mechanical-systems). MEMS are usually made of silicon, but sometimes other materials such as GaAs or diamond are used. They have many technological applications, ranging from accelerometers in airbags and microphones in iPhones to more surprising objects such as electro-mechanical chips dedicated to biology. On the other hand, NEMS are mainly a subject of fundamental research at present because of fabrication and measurement difficulties.
The mechanics of these micro and nanoscale objects is obviously interesting: we can study relaxation and non-linear phenomena for example. But why study these systems at ultra-low temperatures? For three reasons, which correspond to our research projects:
Ideal Conditions
At low temperatures the physical conditions are well controlled and conducive to high quality measurements: the electrical noise is lower than at ambient temperature, the vacuum in the experimental chamber is excellent, the attainable magnetic fields are higher, and superconducting materials can be used. Finally, the physical properties of the materials themselves are often better (less mechanical dissipation, greater stiffness) and easier to interpret (only low energy states are populated). Thus, whatever the micro or nano-mechanical properties studied, the physical conditions are ideal.
Probes
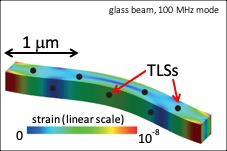
Micro and nanomechanical systems can serve as probes for low temperature physics. They can be used to study superconductivity, for example, by measuring the magnetic force experienced by a superconducting structure when it is subjected to a magnetic field. For our studies, what interests us is to use MEMS and NEMS to probe quantum fluids and the mechanical properties of the solid materials that constitute them. For example, the mechanical dissipation of energy at low temperatures is governed by the quantum tunneling of two-level systems present in structures. This physics, linked to the physics of glasses, is only partially understood in NEMS.
In the study of quantum fluids, mechanical oscillators are often used as viscometers. If the temperature dependence of the viscosity of the fluid is known, the mechanical oscillator can then be used as a thermometer. This viscosimetry of quantum fluids has also recently developed towards quantum turbulence [1]. The mechanical resonator can both generate this turbulence and detect it. Finally, with NEMS it is now possible to probe the superfluid 3He at a length scale of the order of its coherence length x0, which is essentially the size of the Cooper pair which represents the very particular quantum state fluid. We are interested in the low temperature mechanical characterization of these oscillators (typically from 100 µK to 30 K). Preliminary tests in 4He were carried out [2], as well as in superfluid 3He-B in collaboration with Lancaster University.
As an alternative to conventional approaches, the Helsinki team also proposed using quartz tuning forks (the same as those used for the time base of watches) for the study of quantum fluids. Many teams have adopted them because of their ease of use.
Beyond the study of (quantum) fluids at low temperature, viscosimetry, and precision thermometry, the realization of silicon oscillators with rather special geometries has as a direct (« technological ») application in the ULTIMA project (detection of dark matter), by optimizing superfluid 3He bolometers.
As an example, here is a micrograph of a vibrating silicon wire [3].

Microfabricated silicon vibrating wire for thermometry in 3He-B. Its mechanical characteristics are excellent.
Such oscillators could replace conventional vibrating wires to produce high performance thermometers around 100 µK.
These oscillators are made from a silicon wafer, in which a window has been chemically etched, leaving only a thin membrane on one side (typically 10 µm thick). This membrane is covered with metal, and structured by reactive ion etching (RIE). The oscillating structure is the silicon « goal post », covered with a layer of metal (here niobium, a low-temperature superconductor).
Model Sytems
MEMS and NEMS studied at the lowest temperatures are above all model systems for those interested in mechanics per se [4]. Non-linear dynamics, an extremely rich field, can be studied there under optimal conditions. In the case of NEMS, the resonance frequencies are very high (from 1 to 100 MHz typically). Different geometries and materials are used, e.g., silicon goal-posts and doubly clamped silicon nitride beams (see images below ). The latter material has demonstrated exceptional mechanical properties, and is now widely used by the NEMS community.
If the temperature T is high with respect to the resonance frequency characteristic of a mechanical mode ωn, then many phonons populate the mode in question and its dynamics will be described by classical mechanics. Conversely, when kBT << ħωn, the mechanical mode reaches the quantum limit. The different fundamental aspects of these two regimes are discussed below.
Here is a nanomechanical silicon wire.

NEMS of the same geometry as the micro-oscillators already studied. The width and thickness of the structure is 200 nm and the length is approximately 10 μm.
These oscillators are made from an SOI (silicon on insulator) wafer whose sacrificial oxide layer is etched by hydrofluoric acid (HF). A full layer of aluminum is deposited to contact the system. The sample was fabricated in collaboration with Olivier Bourgeois of the Institut Néel. At the top the gate electrode is separated from the oscillator by a gap that can be reduced to less than 100 nm.
Here is a doubly clamped beam NEMS.

Highly strained silicon nitride NEMS in the form of a doubly clamped beam. The width and thickness of the structure is 200 nm and the length is about 15 µm.
These oscillators are made from a silicon wafer covered with highly strained silicon nitride. The silicon is etched with very high selectivity by XeF2 gas. An aluminum metal layer is deposited to form the electrical contacts.
Model systems: micro and nano-mechanics at low temperature
When (at least) one dimension of the system is submicron, we reach the realm of nanomechanics. Several questions are posed by these new objects, for example: do theories that are valid on large length scales successfully explain the mechanical behavior of these tiny devices? Can we again explain the non-linear regimes of these nanobeams in simple manner? How shall one describe thermal transport in this reduced dimensionality at the lowest temperatures? What does happen when these mechanical oscillators are cold enough to be in their quantum ground state?
Our team is developing this path, in collaboration with Olivier Bourgeois from the Institut Néel (thermodynamics group for small systems). Some of these questions have already some answers, and some are still debated today. The mechanical structures can be actuated by the Lorentz force (as for a vibrating wire), or by using an electrical force generated by a voltage applied to a gate electrode close to the structure (see SEM images above). The detection can reach the quantum limit when an optomechanical setup is used (see Techniques). In these studies, temperature becomes a control parameter that tells us about the underlying physical mechanisms: the richness of the thermodynamic baths, but also how fundamental theorems (eg fluctuation-dissipation) do apply.
Quantum ground state
Certainly the most challenging experimentally, but also for our minds, is when one of these mechanical objects is cooled so low that the lowest mechanical mode reaches its ground state of motion, ie its thermal population n < 1. Then all the higher modes are also well in their quantum ground state: the whole micron-sized object (in its largest dimension) is behaving as a quantum object!
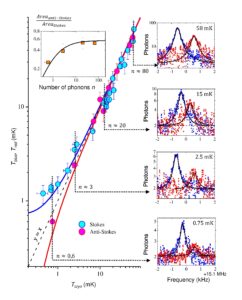
Sideband assymetry measurement from ref. [5] on a 15 MHz flexural drum mode. The height change in the peaks is a direct proof of cooling, see populations n quoted on the graph.
In a collaborative work with colleagues from Aalto (M. Sillanpää’s group) and Nottingham (A. D. Armour), we demonstrated the ground state cooling of an aluminum drumhead device of 15 µm diameter, cooled to 500 µK [5]. The demonstration is done by monitoring so-called optomechanical sideband assymetry at the lowest temperature, which leads to an in-built (almost) primary thermometry (see Fig. above and optomechanics explanations in Techniques). This unique experiment is the first « proof of concept » that it is indeed possible to study a whole macroscopic mechanical device in its quantum ground state, in-equilibrium with its environment. The technological challenge is that it requires to cool the lowest frequency modes to their ground state… And since these modes are MHz, it requires sub-milliK temperatures. Our colleague Miles Blencowe (Dartmouth University) created a « sonification » file of the ground-state cooling track we measured; see our Data Repository link on the left.
In this work [5] we also reported on the fluctuations that the mechanical mode displays: in frequency position, relaxation rate and population. These are not yet understood, but they give us invaluable information about the thermodynamics baths to which the mechanics is coupled. These are potentially the elusive Two Level Systems (TLS) which are present inside the device, in the case of aluminum presumably within the oxyde. The study of TLSs is a challenging and exciting field of research that we discuss in the Amorphous Matter tab.
Stochastic Quantum Thermodynamics and Stochastic Collapse Theories
This new microwave/microkelvin platform opens a path toward a new playground for physicists. It takles fundamental questions of quantum mechanics, linked to both basic (quantum) stochastic thermodynamics concepts, and the cross-over from the quantum world to the classical one. « Standard » thermodynamics concerns big ensembles, for which the well known laws of thermodynamics apply. When studying very small systems, the statistical description becomes much more complex because large fluctuations are possible, and the mean is somehow smeared. One gets in all sorts of paradoxes (like the Maxwell demon), which are actually solved by a rigorous mathematical description of these fluctuations: this is the field of stochastic thermodynamics. When the small object is very cold, then quantum mechanics also comes into play. For our macroscopic mechanical mode, one can for instance wonder if it is possible to « see » a single phonon tunneling in-and-out of the mode? What would be the statistical description of this, how would the fluctuation-dissipation theorem look like in such a condition?
With a whole mechanical object that can move a lot in its quantum ground state, one can also think about quantum-mechanics related paradoxes, like the famous Schrödinger cat. Is it really possible to make a NEMS move so much, in a quantum superposed state, that it would be at two places at the same time? Measuring how long such a thing can survive is called quantum (here mechanical) coherence, and they are proposals to do that. Having a whole system cold and thermalized with an environment under control is then extremely valuable, because then the « expected » sources of quantum decoherence are mastered, and can even be tuned in situ. And, they are proposals that such macroscopic quantum states cannot survive very long in reality, because… Indeed, the macroscopic world is classical! Theoreticians are building so-called Stochastic Collapse Theories that put bounds on such phenomena, in order to explain the classical-to-quantum cross-over. These theories are based on modifications of quantum mechanics taking into account an intrinsic source of noise which makes quantum states decohere, and collapse onto the measurable classical ensemble of states. This noise could be due to quantum gravity, which would be a very neat way of joining quantum mechanics to gravity (a link still missing today). With MEMS and NEMS cooled to their ground state of motion, and the ability to measure them without disturbing them too much, and the capability to make them move, while creating specific quantum states, experimental tests of these theories could be imagined. This is a whole new field of research that opens up, then.
[1] D.I. Bradley, D.O. Clubb, S.N. Fisher, A.M. Guénault, R.P. Haley, C.J. Matthews, G.R. Pickett, V. Tsepelin, and K. Zaki, Emission of Discrete Vortex Rings by a Vibrating Grid In Superfluid 3He-B : A Precursor to Quantum Turbulence, Phys. Rev. Lett., 95, 035302 (2005); R. Hänninen, M. Tsubota, W. F. Vinen, Generation of turbulence by oscillating structures in superfluid helium at very low temperatures, Phys. Rev. B 75, 064502 (2007).
[2] Eddy Collin, Laure Filleau, Thierry Fournier, Yuriy M. Bunkov and Henri Godfrin, Silicon Vibrating Wires at Low Temperatures, J. of Low Temp. Phys., 150, 739 (2008).
[3] S. Triqueneaux, E. Collin, D.J. Cousins, T. Fournier, C. Bäuerle, Yu.M. Bunkov, H. Godfrin, Microfabrication of silicon vibrating wires, Physica B, 284, 2141 (2000)
[4] A.N. Cleland, Foundations of nanomechanics, Springer (2003).
[5] D. Cattiaux, I. Golokolenov, S. Kumar, M. Sillanpää, L. Mercier de Lépinay, R. R. Gazizulin, X. Zhou, A. D. Armour, O. Bourgeois, A. Fefferman & E. Collin, A macroscopic object passively cooled into its quantum ground state of motion beyond single-mode cooling, Nature Comm. 12, 6182 (2021).
Amorphous Matter
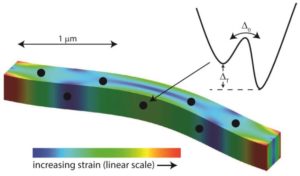
Schematic of a nanobeam containing two-level systems (TLS), whose dynamics are described by a double-well potential.
One of the themes pursued by the group is the study of amorphous materials at the lowest temperatures. These materials, which are found in everyday life due to many of their unique properties, are still poorly understood on a microscopic scale. Paradoxically, although glasses are like liquids in that they do not have long range order, they are rigid.
The low temperature properties of glasses are particularly intriguing. Below 1 Kelvin, the thermal and mechanical behavior of glasses is very different from that of crystals, and it implies the existence of a certain type of low energy excitation (LEE) which is not present in crystals. It is known that these LEEs are generally not impurities, but are intrinsic to glass because the same low temperature characteristics are also observed for ultra-pure specimens.
The true identity of these LEEs is a long-standing question still open today. The most discussed candidates are two-level systems (TLS), which can « tunnel » between two quasi-equivalent energy states (see figure above) [1]. But they have only been identified in certain materials so far. In addition, the mechanical dissipation in amorphous solids is remarkably universal around the 1 kelvin, varying only by about an order of magnitude in the quality factor Q-1 ~ 3 × 10-4 despite enormous variation in composition, impurity concentration and structure.
Solving these puzzles has been a daunting task that has occupied physicists for decades. We address these problems using a range of low temperature techniques, from proven techniques (such as the « Double-Paddle Oscillator », a micro-mechanical structure on which an amorphous film is deposited) to radically new approaches.
Low temperatures are achieved using dilution cryostats in combination with nuclear adiabatic demagnetization. An ultimate goal is to individually control the TLS present in the material, in a coherent way (in the quantum sense). To do this, the amorphous material must constitute a nano-mechanical resonator operated in its fundamental quantum state, below 1 mK (see figure above).
[1] W. A. Phillips, « Two-level states in glasses », Rep. Prog. Phys. Vol. 50, pp. 1657-1708 (1987).
Quantum Fluids & Solids
“Quantum Fluids and Solids” traditionally designates an area of Low Temperature Physics investigating the properties of liquid and solid phases of helium and hydrogen. Helium, in particular, has two stable isotopes, 4He (the usual helium) and 3He, a rare isotope produced in nuclear reactions. The difference between these isotopes is just a neutron in the nucleus, but this apparently harmless difference is in fact essential, as Quantum Mechanics tells us. In Nature, particles can be classified in two families according to their “spin”, and it turns out that 4He is a Boson (its total spin is 0), while 3He is a Fermion (its total spin=1/2).
Their properties are vastly different: 4He displays at low temperatures Bose-Einstein Condensation (macroscopic occupation of the lowest energy state) and it also becomes superfluid, i.e., its viscosity vanishes, an effect observed at a temperature of 2.17 kelvin. The Fermionic isotope, 3He, forms a Fermi Liquid (the occupation of each microscopic state is limited to one), and superfluidity appears only at extremely low temperatures, on the order of 2 millikelvin, by a mechanism involving the formation of “Cooper pairs”.
Quantum effects are thus exacerbated in the dense phases of these very light elements, allowing the observation of quantum phenomena not only at the atomic level, but in large systems: superfluidity is a coherent behavior of a macroscopic number of atoms!
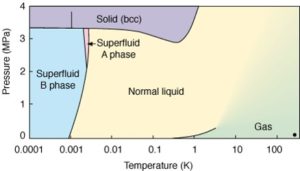
Phase diagram of liquid 3He (A and B superfluid phases)
Helium remains liquid even at the absolute zero of temperature. This surprising behavior is also explained by Quantum Mechanics: for very light atoms, the attractive forces between atoms only provides a weak potential energy, the binding effect of which cannot compensate the large kinetic energy due to the Heisenberg principle: in the solid, the localization of the atoms (position) would excessively increase their momentum. Solidification of helium can still be achieved, however, but this requires applying pressures on the order of 3 MPa.
Helium is an important research subject by itself. In addition, it paves the way to understand other systems, in general rather complex, by providing a convenient simple experimental and theoretical model. This is the case, for instance, for Bose-Einstein Condensation (later observed in atomic gases), superfluidity (as in neutron stars), Fermi Liquids (3He explaining the behavior of metals), and superfluid 3He, opening the way to unconventional superconductivity.
In our Ultra-low Temperature Group, important results have been obtained combining our expertise in low temperatures with other powerful techniques:
NMR at Ultra-low temperatures and fundaments of magnetism
– Experimental proof of Dirac’s Multi-spin exchange (also called “Ring Exchange”) by experiments on bulk and two-dimensional solid 3He (namely helium adsorbed on a very flat surface, see below). Dirac’s multi-spin exchange concept has been applied since then to High-Tc superconductors, organic magnets, and more generally to the Many-Body theory of correlated Fermions.
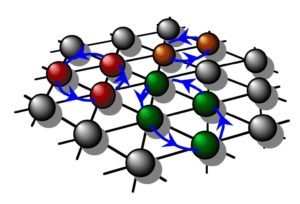
Artist view of multiple spin exchange in 2D solid 3He
– The discovery of two-dimensional nuclear magnetism, observed in 3He films of atomic thickness adsorbed on a graphite substrate. The ferromagnetic system constitutes the first and the most accurate experimental model system for a Heisenberg 2D ferromagnet. The antiferromagnetic system provides, in turn, a textbook example of spin-liquid, where quantum frustration is due to multi-spin exchange.
– The experimental determination of the magnetic Landau parameters of bulk and two-dimensional liquid 3He, a model system for correlated electrons.
Particle detection in superfluid 3He and the Cosmological theory of phase transition
– A superfluid 3He particle detector for the direct detection of Dark Matter has been developed, and shown to provide an excellent sensitivity in laboratory tests (detection of muons, neutrons and conversion electrons).
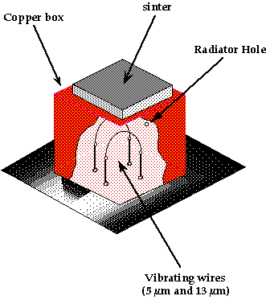
Bolometer for particle detection in superfluid 3He
– Experiments with ultra-sensitive bolometric particle detectors performed at record temperatures below 100 microkelvin) allowed us to achieve a detailed verification of the Kibble-Zurek theory of second order phase transitions. This result had a strong impact, since the dynamics of second order phase transitions is an important field of Cosmology and Condensed Matter physics.
Neutron scattering at very low temperatures: structure and excitations of quantum matter
– The structure of two-dimensional solid helium (3He and 4He) films has been determined by neutron diffraction, contributing to the determination of the corresponding phase diagrams.
– The first direct observation of ripplons, the quantized surface waves which constitute the elementary excitations of the helium surface, and the measurement of their dispersion relation by inelastic neutron scattering.
– The determination of the dynamic structure factor of bulk liquid 3He, and the detailed mapping of the quantum excitations of this Model Fermi Liquid: zero-sound and paramagnons.
– The observation of coherent zero-sound elementary excitations in the spectrum of two-dimensional liquid 3He, beyond the particle-hole band. We suggested that the existence of a well-defined roton-like minimum in the dispersion relation could provide a novel mechanism of High-Tc superconductivity (highQ-plasmon mediated pairing).
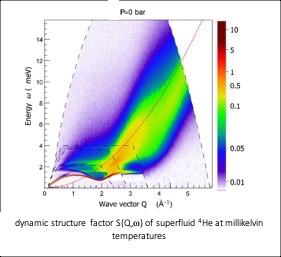
– The thermal properties of complex condensed matter systems can be described by effective theories, as shown by Landau for the model system superfluid liquid 4He. The elementary excitations are described by a dispersion curve of strong and sharp “single excitations”, and a weak continuum of multi-excitations. We have investigated this system in detail by inelastic neutron scattering, and compared the results to the most accurate theories. This recent work shows in particular that the effective description with the measured dispersion relation allows to obtain the thermodynamical properties (specific heat, normal density, etc.) with a better accuracy that the standard thermal measurement of such properties.

Dynamic structure factor of superfluid 4He: a weak continuum of “multi-excitations” is observed above the dispersion curve of single excitations. Their origin can be traced to combinations of single-excitations, for instance “two-Rotons”, “Maxon+Roton, etc…
Selected publications
« Dispersion relation of Landau elementary excitations and thermodynamic properties of superfluid 4He », H. Godfrin, K. Beauvois, A. Sultan, E. Krotscheck, J. Dawidowski, B. Fåk, and J. Ollivier, Phys. Rev. B 103, 104516 (2021). Editor’s choice.
« Microscopic dynamics of superfluid 4He: A comprehensive study by inelastic neutron scattering », K. Beauvois, J. Dawidowski, B. Fåk, H. Godfrin, E. Krotscheck, J. Ollivier, A. Sultan, Phys. Rev. B 97, 184520 (2018).
« Observation of a roton collective mode in a two-dimensional Fermi liquid », H. Godfrin, M. Meschke, H.-J. Lauter, A. Sultan, H.M. Böhm, E. Krotscheck, M. Panholzer, Nature 483, 576–579 (2012).
« Ferromagnetic nanoclusters in 2D-3He », E. Collin, C. Bäuerle, Yu. M. Bunkov and H. Godfrin, Phys. Rev. B 73, 125421, (2006).
« The Magnetic Susceptibility of Liquid 3He », H. Godfrin, in « Introduction to Modern Methods of Quantum many-Body Theory and their Applications », Series « Advances in Quantum Many-body Theories », Vol. 7, Chapter 8, p.329, Ed. A. Fabrocini, S. Fantoni and E. Krotscheck, World Scientific (2002).
« Quantum frustration in the ’spin liquid’ phase of two-dimensional 3He », E. Collin, S. Triqueneaux, R. Harakalay, M. Roger, C. Bauerle, Yu.M. Bunkov, H. Godfrin, Phys. Rev. Lett. 86, 2447-2450 (2001).
« Multiple-Spin exchange on a triangular lattice: a quantitative interpretation of thermodynamic properties of two-dimensional 3He », M. Roger, C. Bäuerle, Yu.M. Bunkov, A.S. Chen, H. Godfrin, Phys. Rev. Lett. 80, 1308-1311 (1998).
« Laboratory simulation of cosmic string formation in the early Universe using Superfluid 3He », C. Bäuerle, Y. Bunkov, S.N. Fisher, H. Godfrin and G.R. Pickett, Nature 382, 332-334 (1996).
« Ripplons in 4He films observed by neutron scattering », H.J. Lauter, H. Godfrin, V.L.P. Frank and P. Leiderer, Phys. Rev. Lett. 68, 2484-2487 (1992).
« Two-dimensional nuclear magnets », H. Godfrin and R.E. Rapp, Advances in Physics 44, 113-186 (1995).
« Experimental Properties of 3He adsorbed on Graphite », H. Godfrin and H.J. Lauter, in « Progress in Low Temperature Physics », Vol. XIV, Chapter 4, p; 213-320, by W.P. Halperin, Elsevier Science B.V., Amsterdam (1995).
« Experimental observation of a two-dimensional Heisenberg ferromagnet », H. Godfrin, R. Ruel, D.D. Osheroff, Phys. Rev. Lett. 60, 305-308 (1988).
« Multiple spin exchange calculation of the T = 0 properties of solid 3He », H. Godfrin, D.D. Osheroff, Phys. Rev. B 38, 4492-4503 (1988).
Cryogenics
The Ultra-low temperature team is depositary of the sub-milliKelvin nuclear demagnetisation technology at CNRS. Besides, the team possesses two commercial (« dry ») dilution cryostats that reach base temperature of 8 mK. These machines are autonomous and do not require liquid helium to cool down: they have a pre-cooling stage based on a pulse-tube cooler reaching about 3 K. They work on the same principle as « wet » machines to reach the sub-Kelvin range: the dilution of 3He into 4He. A schematic of the principle is given below:
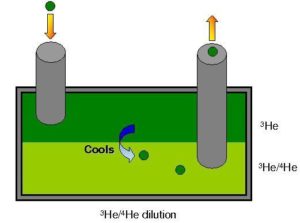
This represents the so-called « mixing chamber » of the cryostat. This is the place where the mixture separates in a pure phase of 3He (dark green) floating on top of a heavier phase of 4He containing about 6% of dissolved 3He (light green). By means of a pumping system (at room temperature), a flow of 3He is forced through the machine (yellow arrows). When these atoms cross the boundary and dilute into 4He, they absorb heat: the cooling power of this mechanism goes at low temperatures as dn/dt T2 with dn/dt the flow of 3He atoms and T the mixture temperature. Our machines typically have 20 µW of cooling power at 20 mK. More information can be found in e.g. F. Pobell, Matter and Methods at Low Temperatures, Springer (2007).
Our team has also a home-made nuclear adiabatic demagnetization cryostat that reaches temperatures of the order of 100 µK, and is developing a second such equipment. The machine is built around a first stage that is a conventional dilution unit, connected through a « heat switch » to the « copper nuclear stage ». A picture of the cryostat is shown below, with its plastic mixing chamber and the copper stage underneath it. The microwave wiring of our experiments is also visible.

The heat switch is made of a piece of aluminium inserted in a small coil. When there is no current in the coil, the aluminium is free of magnetic field and superconducting: it does not conduct heat (the switch is « open »). When we pass a small current in the coil, a small field applied on the aluminium makes it normal: it is then a very good metal conducting heat (it is « closed »).
The technique is single-shot: one first pre-cools the copper stage in a high magnetic field Bini (about 7 T), with the heat switch « closed ». This takes about a week to reach Tini ≈ 10 mK. By doing so, the spins carried by the copper nuclei get polarised. Then the heat switch is « opened », and the magnetic field is very slowly decreased down to Bfin. This process is adiabatic, which means that it takes place at constant disorder (entropy): the spins remain polarized, which means that the temperature has to decrease to Tfin. This is illustrated on the drawing below.
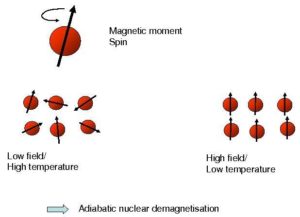
If the process is ideal, it verifies Bini /Bfin = Tini /Tfin. Therefore, demagnetising down to 70 mT cools the system down to 100 µK. More information can be found in e.g. F. Pobell, Matter and Methods at Low Temperatures, Springer (2007).
One important component of cryogenics, besides cooling techniques, is thermometry. It is indeed mandatory to control what is the actual temperature of different places within the cryostat (including of course the sample!), and also to manage the heat loads. Obviously, the colder we are, the more difficult this task is. Above 4 K, one can use the electrical resistivity of a piece of metal (in this case, platinum) to work out the temperature. In the dilution temperature range (down to 10 mK), one can use non-metallic probes like carbon resistors which value will grow substantially as they cool. The measurement has to be done very reliably, at the lowest possible injected power (in order not to heat). This is performed using resistance bridges, connected with 4 wires to the probe. Below 10 mK, thermometry becomes very difficult. We use a home-made 3He thermometer: a quartz tuning fork immersed in the liquid that measures its viscosity. This is shown on the graph below.
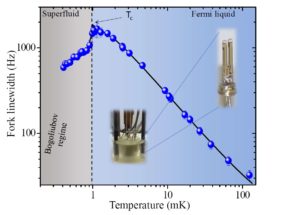
The properties of 3He are well known and tabulated; this makes this device very reliable. 3He becomes superfluid below Tc ≈ 1 mK (BCS pairing of Fermions). Above this temperature, it is a Fermi liquid. More on thermometry can be found in e.g. F. Pobell, Matter and Methods at Low Temperatures, Springer (2007).
The Ultra-low temperature group works in close contact with the cryogenics team of Néel. We participate in new technological developments, like nuclear demagnetisation adapted to dry cryostats. Many other technological aspects are tackled by the team, like e.g. microwave optomechanics. As such, we possess a bunch of 4 K liquid helium cryostats, and many other mandatory pieces of equipment (noise SQUID thermometers, primary pressure gauges, lock-in detectors, …).
Microwave Optomechanics
Micro and nano electro-mechanical systems (MEMS and NEMS) can be actuated and detected by various means. Not relying on specific materials properties, the simplest are capacitive and magnetomotive schemes, which only require the device to be (at least partially) conducting.
For capacitive, the moving element is coupled to a gate electrode C on which a voltage V=Vdc+Vac cos(ω t+Φ) is applied. Since the total capacitance C(x) depends on the motion x, this creates a force F= d/dx [1/2 C(x) V2] (which is usually non-linear, i.e. it depends on x). The motion can in turn be detected by the modulated current that flows through the capacitor, I = d/dt [C(x) V].
For magnetomotive, a current I=Iac cos(ω t+Φ) is fed into the structure which is immersed in a static magnetic field B0. A Laplace force then acts onto it F= I li B0 (with li the length of the path taken by the current). This force is essentially linear, i.e. it does not depend on x. The motion of the conductor length li cuts the magnetic field lines which induces a voltage (Lenz law) V= – B0 li d x/dt, which can be detected.
These techniques are rather straightforward, and require typically just a generator and a lock-in detector. However, because of the finite impedance of these apparatuses, the mechanical motion is usually loaded by the circuit: there is an extra damping acting on the mechanical resonance due to dissipation of energy in the electric circuit. As well, the resolution of these techniques is usually not very good; it is for instance impossible to resolve Brownian motion.
On the other hand, coupling moving objects to light is an extremely efficient way of actuating/detecting the motion: this is the field of optomechanics. One can detect Brownian motion, and the detection scheme is even quantum-limited (i.e. it reaches the ultimate limit fixed by Heisenberg’s uncertainty principle). But high intensity laser light is not very compatible with cryogenics; for this reason, microwave optomechanics is much more adapted.

The moving object is here coupled to an RLC circuit which acts as an optical cavity. The mechanical device modulates the capacitance C of the mode: this is a parametric coupling, i.e. the motion changes the resonance frequency of the microwave resonator. In practice, the cavity is coupled to a microwave transmission line, with one or two ports. It can thus be measured by sending a microwave signal into the line, and looking at the reflected/transmitted signal. This is what performs e.g. a Vector Network Analyser, see image above. More on microwaves can be found e.g. in D.M. Pozar, Microwave engineering, John Wiley and Sons (2012).
The modulation C(x) by the motion x(t) imprints sidebands in the measured spectrum. The simplest schemes that can be used are single-tone measurements, where a pump tone is applied at a frequency ωcav+Δ (with ωcav the microwave cavity resonance frequency) and Δ=0,+Ωm,-Ωm (with Ωm the mechanical mode resonance frequency). The schematic below represents the case where the microwave cavity linewidth κ << Ωm (so-called sideband resolved).
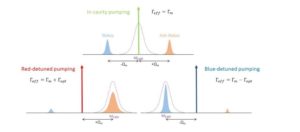
When the pump tone is applied at the cavity frequency (Δ=0), two equivalent sidebands appear on both sides, shifted by +-Ωm. The peak area is directly linked to the energy stored in the mechanical mode, and its width is given by the mechanical damping rate Γm.
If now the pump tone is applied at Δ=-Ωm (red detuned), the lower sideband (Stokes) is strongly suppressed and only the one at ωcav is measured. This scheme allows to transfer energy from the mechanics to the optics: the mechanical mode can be (actively) cooled, and its damping Γeff is increased.
Reversely, when Δ=+Ωm (blue detuned), the lower sideband is measured (and the Anti-Stokes suppressed). In this case, energy can flow from the optics to the mechanics, and the mode heats up (or equivalently, the motion is amplified). At the same time, the mechanical damping Γeff is reduced. For both red and blue detuned schemes, the efficiency of the cooling/heating depends on drive power through Γopt ∝ Pin.
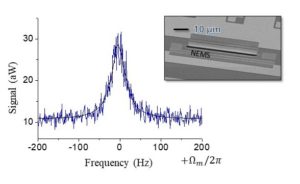
On the graph above, we show an example of Brownian spectrum measured with blue detuned scheme at 200 mK on a 50 µm long SiN/Al beam device resonating around 4 MHz (cross-section 300×100 nm2). More on optomechanics can be found in M. Aspelmeyer, T.J. Kippenberg, F. Marquardt, Cavity Optomechanics: nano- and micromechanical resonators interacting with light, Springer (2013).
Training
As part of its duties, the ULT group is organizing Schools & Conferences over the years. The list can be found below, with extra information (use the links) like list of contributors/participants, and some available talks. A regular training session is the European Advanced Cryogenics School, which is organised today in the framework of the European Microkelvin Collaboration (EMP).
Cryocourse 2021 European Advanced Cryogenics School, Grenoble 2021
LANEF Demag Day (see link in side panel): Electronic and Nuclear Demagnetization Refrigeration, Grenoble 2021
ULT 2014 Frontiers of low temperature physics, Bariloche (LT27 satellite conference)
Cryocourse 2013 European Advanced Cryogenics School, Grenoble 2013
Cryocourse 2011 European Advanced Cryogenics School, Grenoble 2011
Quantum Fluids and Solids QFS 2010 International Conference, Grenoble 2010
Cryocourse 2007 European Advanced Cryogenics School, Grenoble 2007
Workshop on Dark Matter Search and Related Topics Workshop JSPS-CNRS Collaboration, Grenoble 2007
Disorder and topological defects, a Helium primer COSLAB Workshop, Chamrousse 2004
Topological defects and the non-equilibrium dynamics of symmetry breaking phase transitions ESF Network and Winter school, Les Houches 1999
Workshop on the formation of topological defects ESF Network, Grenoble 1997
LANEF Demag Day
Electronic and Nuclear Demagnetization Refrigeration
9:30-17:00 on 20 September 2021
Location: Institut Néel/CNRS
This workshop was devoted to advances in adiabatic demagnetization refrigeration (ADR) and to exploring connections between the fields of nuclear and electronic ADR.
For more info: andrew.fefferman@neel.cnrs.fr
Speakers with links to selected presentations:
Jean-Marc Duval (CEA): Electronic ADR: applications in space and on land
Lionel Duband (CEA): Hybrid subkelvin cooler for the ATHENA mission
Philippe Camus (Institut Néel): EasyCool–Continuous magnetic refrigerator
Mike Zhitomirsky (CEA): Frustrated magnets and other cool materials
Edward Riordan (Institut Néel): Magnetocaloric materials
Christophe Marcenat (CEA): Implementing ADR on PPMS
Guillaume Donnier-Valentin (Institut Néel): Superconducting coils
Juha Tuoriniemi (Aalto University): Nuclear demagnetization refrigeration
Andrew Casey (Royal Holloway University): Nuclear demagnetization on dry dilution refrigerators
David Schmoranzer (Charles University): Simulations of continuous nuclear demagnetization refrigerators
Sébastien Triqueneaux (Institut Néel): Development of a continuous nuclear demagnetization refrigerator
Alumni
Ketty Beauvois, Instrument Scientist, Institut Laue Langevin.
Yuriy Bunkov, former permanent staff, now at Kazan.
Dylan Cattiaux, Engineer, Absolut System.
Anna Isabel Maldonado Cid, Ministry of Economic Affairs and Digital Transformation, Spain.
Martial Defoort, permanent CNRS researcher at TIMA.
Johannes Elbs, Engineer, Infineon Technologies.
Rasul Gazizulin, Assistant in Research, National High Magnetic Field Laboratory, USA.
Pierre Hunger, Professeur de sciences physiques CPGE.
Yuriy Krupko, Research Engineer, LNCMI Grenoble.
Sumit Kumar, postdoc at Royal Holloway University of London.
Gwenvredig Le Roy, PhD student at TU-Wien.
Annina Luck, Volume Graphics.
Olivier Maillet, permanent CEA researcher at CEA-Saclay.
Richard Pedurand, research engineer at Renaissance Fusion, Fontaine (France)
Mgcini Keith Phuthi, Ph.D. student in Mechanical Engineering at Carnegie Mellon University, USA.
Thomas Prouvé, research engineer, CEA Grenoble.
Matthias Raba, researcher, CEA Grenoble.
Kunal Lulla Ramrakhiyani, Experimental Officer at the Quantum Technology Centre in the Physics Department and Manager of the Nanofabrication facility, Lancaster University, UK.
David Schmoranzer, professor at Charles University.
Ahmad Sultan, Optronic Detectors Architect, LYNRED.
Emily Thomson, engineer at Raytheon, Lompoc, California.
Xin Zhou, permanent researcher at IEMN, CNRS.
Funding
Within our Host Institution CNRS, our research is funded essentially by two main sources: these Funding Agencies are National (ANR), and mostly at the European level (ERC). Beyond the StG and CoG grants the group received, the ULT team is part of a European Infrastructure that federates Ultra-Low temperature physics (and technologies) at the European level.
ANR MORETOME (2023-2026): Part of this project, which is lead by IEMN in Lille, is to develop a platform to perform smart sensing with more than one mechanical device coupled to microwave photons. Such an optomechanical resource could help characterize Brownian and quantum fluctuations at ultra-low temperatures, and understand other sources of fluctuations, especially impacting more than one mechanical mode (through correlations).
ERC PoC NewCooler (2023-2024): A European Proof of Concept grant devoted to constructing a continuous nuclear demagnetization refrigerator (CNDR). Reaching temperatures near 10 mK has become relatively easy in the last decade. This cryogenic advance has driven an explosion in industrial efforts to build quantum computers based on superconducting qubits as well as rapid progress in fundamental physics experiments around 10 mK. However, cooling condensed matter below 1 mK remains challenging. The CNDR will solve this problem by maintaining the sample temperature below 1 mK indefinitely while providing a large experimental space and eliminating the need for a liquid helium supply. We expect the CNDR to allow rapid investigation of qubits whose coherence is enhanced at temperatures << 10 mK and to propel work in fields ranging from nanomechanics to topological superconductivity.
ERC StG UNIGLASS (2017-2023): This European Starting grant is focused on the enigmatic universality found in low temperature properties of amorphous materials. The ultimate aim of this project is to be able to manipulate the quantum state of single low-energy states that are supposed to be at the origin of the unique properties of glasses (so-called Two-Level Systems).
H2020 infrastructure EMP (2019-2023): This is the Infrastructure grant that takes over Microkelvin (see below). The consortium is made of 17 partners, among which are 8 universities, 3 associated institutes, and 6 private companies. The eight European laboratories at the core of EMP all possess the capabilities to reach sub-milliKelvin temperatures; they are custodians of these technologies in Europe.
ERC CoG ULT-NEMS (2014-2021): In this Consolidator grant, following the ANR QNM project, the focus is on quantum properties probed by nano-mechancial resonators cooled down to ultra-low temperatures. Two aspects are dealt with: the microscopic scale (with elementary excitations from the surrounding baths that can couple to the mode under study), and the macroscopic one questioning basic concepts of Macroscopic Quantum Mechanics.
FRP7 Microkelvin (2009-2013): Infrastructure grant that links together all ultra-low temperature laboratories from Europe. CNRS Grenoble was one of the 3 founders of this consortium. This activity has been prolongated through EMP (see above).
ANR MajoranaPRO (2013-2018): ANR project aiming at the study of exotic excitations present in superfluid 3He in confined conditions (so-called bound states). In particular, within the B-phase of the superfluid, these states are theoretically demonstrated to be Majorana (quasi-)particles.
ANR QNM (2010-2014): This ANR grant enabled to launch the ultra-cold MEMS and NEMS activity within the ULT team. The activity continued then within the ERC ULT-NEMS (see above).
ANR High-Q Fermions (2010-2014): This ANR research project aimed at studying elementary excitations in liquid helium with large Q wave-vector, by means of neutron spectroscopy.
ANR ULTIMA (2005-2008): ANR funded research project that evaluated the capabilities of 3He superfluid bolometers for the search of cold dark matter.



Data Management Publications
Experimental results published within the EMP consortium are published within green or gold open access. The data published is also made freely available to the interested readers:
To access these data, follow this link.
The « sonification track » of the ground-state cooling run [Cattiaux et al., Nat. Comm. 12, 6182 (2021)] can be found following this link; special thanks to Miles Blencowe (Dartmouth) for this!
The typo-corrected version of Dylan Cattiaux’s PhD manuscript (UGA and GDRMecaQ prize awards) is available: link to CattiauxPhD2021.pdf
Cryogenics Database
A Cryogenics Database has been put together by the EMP consortium. It can be consulted here: Cryo-tools EMP.